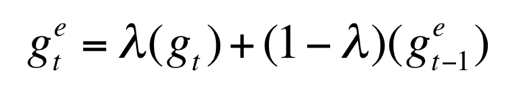Learning about the Money Multiplier model with Steve Keen

I know that many economists dismiss Steve Keen as a crank (and by “crank” I mean an unserious thinker who refuses to subject their views to an honest critique) but I respect and admire the way he draws upon heterodox ideas and forms compelling narratives. So I was grateful to him for a recent dialogue that we’ve had on X.

(Since X requires you to be logged in to view posts, and because some of the threads can be hard to keep track of, I will post screenshots below. If Steve chooses to reply to this article I would hope that he acknowledges that these are all genuine posts and that I have represented his statements fairly).

It began by him joining a thread that he was tagged in, and being rude about George Selgin.

George is an economist who I admire deeply and know personally and while he doesn’t need me to defend him, Steve’s accusation piqued my curiosity.

It was clear that Steve was referring to a specific interaction, and once George joined the thread the source of the issue appeared to have been a misunderstanding. Here is what happened:

1. Steve had made a claim about the standard, traditional, textbook version of the Money Multiplier (MM) model.

2. George had made it clear that while not endorsing the MM he objected to Steve’s depiction of it. He laid things out step-by-step.

3. Steve attempted to use his software, Ravel, to reveal a flaw in George’s claims, and therefore in the MM.

Here is a link and a screenshot of Steve’s “proof”:

Note the phrase “precisely what George asserted in his tweet stream”. Indeed, here we see a direct link between George’s tweet and Steve’s output in Ravel:

However, it soon became clear (in part thanks to comments by Andreas and Erik) that George had already corrected himself:

At this point, you do not need to know anything at all about money and banking to understand that Steve had seized upon George’s bad wording and that his conclusion was a result of his (incorrect) interpretation of what George had said, rather than the logic of George’s intended argument.

Erik managed to pin Steve down on this. Here is a summary of their exchange:

Erik: @ProfSteveKeen is there anything wrong with my, and therefore @GeorgeSelgin's, accounting now that all the misunderstandings has been cleared?

Steve: The error is that… Joe gets a liability (debt) with no asset (money) at this point. There is no way around this.

Erik: you’re criticizing a series of transactions that George never meant to suggest… disregard his clumsy sentence regarding lending reserves. I think the transactions in my screen shot above represents George’s step 1 and 2. Do you find anything wrong with THOSE?

Steve: Apart from some poor labelling, no.

Hallelujah! Agreement? Right?

I posted the exchange, praising Steve for accepting that George’s argument was correct. He seemed to want to caveat it by saying that George’s reasoning rested on Post Keynesian ideas, but whatever. My focus was on accuracy, not labelling. So I was puzzled that he subsequently reverted to his accusation that George was wrong.

I found Steve’s stubbornness really interesting. One would expect him to acknowledge George’s clarification and to retract his claim. Instead, he continued to assert that George was wrong without even acknowledging that he had misunderstood him. And he did so by returning to the source of the confusion, which is the precise wording around whether a bank “lend its reserves” or “lends an amount equal to its reserves”. Rather than seize an opportunity for common understanding, he was knowingly making an assertion that is prone to being misunderstood.

So I decided to pursue this. I will provided an edited account of our subsequent exchange, and reiterate that you do not need to understand the economic concepts to understand what is going on here…

Anthony: is your claim that loans have to be in cash contingent on whether there is a mandated reserve requirement?

Steve: No. Regardless of whether there is a mandated reserve requirement or not, to "lend from reserves" as textbooks teach and Fed Reserve Chairs state, the loans must be in cash. The loan can't credit borrower deposit accounts without violating the rules of accounting.

Anthony: Why can't a bank credit a deposit account and thus assets and liabilities offset?

Steve: because it violates the rules of accounting.

Anthony: You're saying that when a bank provides me with a loan it doesn't obtain an asset??

Steve: Of course a bank gets an asset when it provides a loan: the borrower's debt rises.

Anthony: I asked "Why can't a bank credit a deposit account and thus assets and liabilities offset?" You replied "It's because it violates the rules of accounting." And now "Of course a bank gets an asset when it provides a loan" I'm confused.

The problem here is that Steve is fixated on the “textbook” model and believes that I am deviating from it in providing my response. Similarly, he only granted George as being correct if George admits to being a Post Keynesian. Steve’s focus is not on whether George or I are correct, but the textbook model. But here’s the issue: he accuses both myself and George of being mainstream economists who subscribe to that model! Hence my desire to base the discussion around what I think, rather than what Steve and I accept as being the “textbook” account. Clearly, there is a risk that the unspecified and uncited “textbook” account becomes a strawman. And thus Steve’s critique rests on his misinterpretation of certain claims..

Here’s what happened next in the exchange:

Anthony: do you accept that your screenshot from Ravel doesn't actually capture the scenario I provided?

[Note that I’m making it clear that I am talking about my understanding of banking, and not the logic of the MM]

Steve: If the Fractional Reserve Banking model has any meaning, you have to “Lend from Reserves”. I’m saying the model works if and only if loans are in cash.

Anthony: Rather than simply repeat your assertions, can you respond to my question?

He didn’t reply.

So I took the opportunity to post a snarky tweet where I mocked him for suggesting I get a copy of his software.

Then, to his credit, after repeated attempts to point out what he had ignored, he did return to my specific question. Here was the scenario I was talking about:

A bank decides to extend a loan by crediting a deposit account.

Steve showed how that looked in Ravel, and acknowledged that it was different than his first version (link):

All I wanted him to do was to acknowledge that a bank can credit a deposit account without violating the rules of accounting. Not because I thought this was a “gotcha!” but because I thought it was something we agreed on, and could therefore serve as a starting point to interrogate the real issue (which was whether the Money Multiplier story requires all loans to be made in cash). Eventually, we got there (link):

Anthony: do you acknowledge that this is different to the one you showed [previously]?

Steve: Of course I do!

Anthony: so you agree that your original analysis in Ravel didn't balance because you misunderstood the scenario being presented to you (rather than because I had relied on faulty logic).

Steve: No. I modelled lending from Reserves, which plenty of Neoclassicals (maybe including you) have described as non-problematic. I showed that it violates the laws of accounting. But endogenous money as in the Bank of England paper you criticize works just fine.

[Note that Steve is accepting that his first screenshot was based on how he thinks other people view things, not what they actually believe.]

Anthony: But you accept that it was your decision about how to model it, rather than the claim that I was actually making, that meant it didn't compute?

Steve: I was criticising Selgin FFS

Anthony: In this post you seem to be directing your response to me. So: do you accept that the reason the Ravel output doesn't balance is because of an assumption that you made, rather than whether my example makes sense?

Steve: I admit that I am modelling lending from reserves when I show this impossible situation.

Anthony: Can we try to work an example based on what I say, rather than what you think someone else is saying?

Yes, I know I am being pedantic. But at this point Steve tried to turn the tables, and asked me “How on earth do you think Reserves are integral to lending?“ Before following this path, however, I wanted an acknowledgement that Steve’s Ravel output was wrong because of his choice of input, and not the logic of my argument. Here was the breakthrough:

Anthony: I am keen to discuss that point further, but I'm troubled by your inability to acknowledge a very simple point - that your table is out of balance because of your assumption and not because of my example. Can we agree on that please?

Steve: Oh FFS Anthony, it was because George asserted that since banks could buy bonds with reserves, they could also make loans from reserves. I said bollocks to that, and showed why because of George's example, not yours.

So if you want an admission, yes. I was criticising George's assumption, not yours.

To which I triumphantly responded, pleased that my point was made (and could also be extended to how Steve treated George).

With that groundwork laid, I wanted to have a more substantive conversation about the topic. Steve asked me: “So tell me how you think banks make loans”.

I considered this to be a deliberately obfuscatory question, since he didn’t specify whether he was talking about theory (and if so which theory) or practice. Was this Steve’s attempt to move beyond a disagreement about the implications of the MM, and find out what I think?

Part of the problem here is contained in the fact that I referred to the Money Multiplier model. We might instead view it as an explanation, or a depiction. Perhaps even a story. What is notable is that no-one seems to articulate what they are actually talking about. I haven’t yet found an article that quotes directly from a standard economics textbook and explains why it is wrong. So I am skeptical about whether the claim is that it truly is wrong rather than flawed, incomplete, or no longer relevant.

All economists have been exposed to the concept of the MM at some point. There is general agreement about what it is, and I think there is a consensus that (i) it does not accurately explain how the banking system works today; (ii) it wasn’t a completely accurate and literal description of banking practice historically. The point is whether it was useful, as a pedagogical device, to approach the topic of money and credit creation, how policy decisions work through the banking system, etc.

The only mention of the Money Multiplier in my own textbook is this:

The money multiplier shows the change in the number of deposits for a given monetary base, and indicates the effectiveness of the bridge of intermediation.

Which isn’t great but certainly doesn’t form the basis of an explanation for credit creation. In a 2017 paper published in Economic Affairs, I argued that the concept of a “multiplier” is unhelpful and we should think in terms of ratios instead. But even though I’ve published research in this area, I am open minded about the validity of traditional economic concepts and I don’t feel that I have a solid grasp either of the theory or the debate. I approach this issue as a teacher, where my goal is for it to make sense. I am not approaching it as a heterodox economist aiming to distinguish myself from others.

My suspicions of Steve’s conduct, and intentions, can be seen in this exchange.

According to Steve, “George asserted banks could use reserves to make loans”. And yet George said “they can use [reserves] to finance loans”. [Emphasis added]. If the nub of the issue is whether reserves are being used as a direct source of fundings, this might not be a mere quibble. The subtle way in which Steve misrepresented George’s statement may in fact be telling.

I asked Steve to provide some context, because I want to avoid a situation where we spoke at cross purposes. And although I do not think that the monetary regime necessarily changes the logical coherence of the MM model, I felt it was important to agree on whether we were talking about the current system (where banks are not required to keep a certain proportion of deposits as reserves) or the previous system (where mandatory reserve requirements did play a role in monetary policy). So here is the conversation (link):

Anthony: I think the best explanation for how banks make loans depends on the monetary regime (e.g. whether there are mandatory reserve requirements, whether interest is paid on reserves, whether the supply of reserves is a policy objective or not). So I need more context to answer.

Steve: Do banks use reserves to make loans (a) with mandatory reserve requirements and (b) without interest paid on reserves and (c) when the supply of reserves is not a policy objective?

Anthony: I think that depends on what you mean by "use reserves to make loans". Do you agree that there's a difference between (1) immediately passing on newly obtained reserve balances to a customer; and (2) those reserves forming part of their constraint on lending.

Steve: Yes.

Anthony: Ok, and is the latter factually correct?

Steve: No

I found this answer interesting, because I drew a distinction around what I anticipated Steve would object to (that banks use reserves as a direct source of funding for deposits) and what I think is more defendable (that mandatory reserve requirements mean that reserves serve as a constraint on lending). So this was worth pursueing.

Anthony: So what are the main constraints on bank lending, when reserve requirements are mandated, if not reserves?

Steve: The willingness of banks to lever up (when creating loans) relative to their their equity, which is pro-cyclical.

Anthony: And does creating loans affect their reserve ratio?

At this point Steve simply posted a link to a CNBC article by John Carney called “Basics of Banking: Loans Create a Lot More Than Deposits”. I wasn’t sure if this was because he didn’t want to admit that yes indeed creating loans affects the reserve ratio, therefore reserves form part of a constraint on lending, therefore I was right. So I persevered:

Anthony: Are you saying, "yes it does"?

Steve: No it doesn't. But loans can trigger reserve requirements and equity raising after the event. You have the causal sequence backwards.

I didn’t, because my causal sequence started with loans.

Anthony So we agree that lending decisions have to give consideration to reserve balances?

But Steve wouldn’t be drawn! He said:

Steve: “You tell me whether you agree that loans create deposits first.”

I thought I had already dealt with that, so replied:

Anthony: I've already said, "A bank decides to extend a loan by crediting a deposit account". Does that deal with your question?

Which he interpreted to be confirmation that he was right all along and that the conversation was now over.

Steve: Yes. With reserves paying no role. So we’re agreed: banks create money by lending, and the money multiplier, fractional reserve banking, and loanable funds models are all false. Thanks. Now I’ll get in with my day.

But not so fast! We were actually very close to resolving the issue.

Anthony: Do you accept that lending decisions have to give consideration to reserve balances? (particularly in the context of mandatory reserve requirements)

Steve: Yes. They are a classic non-binding constraint, except for banks that are going under, like Northern Rock.

Anthony: Ok, so you accept that reserves *do* form a constraint on lending, but that ordinarily it is non-binding.

At this point the author of the CNBC article jumped in, and asked me:

John: Can you explain how you think they “form a constraint on lending” today? Or even under a reserve requirement system?

And Steve used that as an opportunity to bow out.

Steve: Tag team time... Over to you John!

Note how Steve’s position changed subtly (from “not a constraint” to “a non-binding constraint”) and instead of exploring what this (potentially critical) difference was, he attempted to shift the conversation away from answering my question (twice) and said that he would no longer respond (twice).

Here is my reply to Steve (which hasn’t been answered):

And here is my reply to John (also unanswered):

To be clear - neither of them owe me a response. But it seems telling that just as I feel I am on the verge of identifying an important, detailed point of difference… they go quiet. It is as if their aim is to make a point, rather than to seek common understanding.

I do not think I’ve identified a “gotcha!” here, and getting Steve to shift from “no constraint” to “what sort of constraint” doesn’t make me right and he wrong. But perhaps the fact that he didn’t make this concession implies that it is important. So although in the first conversation (about the Ravel output) I did manage to establish a starting point of agreement, on this occasion I didn’t.

I think I can make sense of things though.

Firstly, there is an issue relating to economic theory. It seems to me that there are really three issues to address:

1. Is the MM internally coherent?

2. Was the MM a useful way to understand the topic in the past?

3. Is the MM the best way to understand things today?

All sides seem to recognise that there are better ways to explain how banks operate today than through the concept of the MM so point 3 is by the by. (And therefore particularly irritating when people jump into a technical discussion about a specific context, such as whether the MM was a coherent concept in a world of mandatory reserve requirements, by arguing that “that isn’t how the present banking system works!”).

I believe that Steve wants to argue against 1, and feels that his reasoning carries over to point 2. And although George was willing to go all the way to defend point 1, I limited my arguments to 2. Indeed, I think this reveals why Steve is so repetitive about the phrase “banks lend from reserves” and so myopic about George’s correction that [banks] “lend an amount equal to its [excess] reserves”. ChatGPT seems to do a helpful job of summarising this issue:

Note that the extent to which that key phrase, “banks lend from reserves” is incorrect is based on a misinterpretation and an oversimplified analogy. But also telling that Steve attributes it to those he seeks confrontation.

The claim that “reserves constrain lending” is considered technically correct, albeit subject to context. This was what I was trying to drill down with Steve. But he did acknowledge that even in a mandatory reserve requirement regime the constraint is only “non-binding” ordinarily.

I think this brings us to the crux of the endogenous money argument. The “modern view” is a function of the monetary regime, and this isn’t fixed. When those who disparage the neoclassical, or mainstream, or MM, or fractional reserve position say things like “the supply curve for reserves is perfectly elastic, therefore they provide no constraint over bank lending” (or words to that effect) they gloss over the fact that this only holds at the designated interest rate. And that this is a policy choice.

This is a point made by George in his working paper, “Banks Are Intermediaries of Loanable Funds” (which I know Steve has claimed to have read, even if he didn’t link to it):

“It is of course true that any central bank interest-rate target implies a reserve supply schedule that’s horizontal at the targeted rate. It’s also true that, as long as it remains committed to a particular target rate, a central bank must allow the stock of reserves to adjust passively with the quantity demanded at that rate. But if monetary policy means anything in a rate-targeting regime, it means that the central bank routinely reconsiders its rate target, shifting the horizontal reserve supply schedule up or down whenever it sees fit to do so for the sake of meeting its macroeconomic objectives; and this ability leaves it no less in ultimate control of the outstanding quantity of reserves than it would be were it to instead target that quantity itself.” (p.33)

It seems to me a bit like saying that fixed exchange rates contain zero exchange rate risk. That’s only true as long as they hold. In a modern regime the profitability of funding opportunities constrain bank lending, but as George said here,

“loans are only profitable if they pay enough to cover banks’ funding costs, including costs of funding settlements—_not_ just the (near zero) cost of crediting borrowers’ accounts!”

I think that if we are arguing about how much of a constraint they are, and under what circumstances, then Steve has conceded the main point.

My second conclusion is that there is an issue here relating to the sociology of economic debate. As with X/Twitter discussions about MMT I have noticed a pattern:

• Appeals to authority

• A clearly cultivated internal language

• A view that “everyone else” is wrong

• A reluctance to enter into the detail of the issue

I consider myself to be a heterodox economist and so I recognise this phenomenon. It can be appropriate to enter a discussion and then pass over to experts once you get out of your depth. (Better than to keep digging a pit full of contradictions and absurdity that reflect your own intellectual gymnastics rather than the ideas you supposed to be grappling with). Amateur economists should be welcome. The elite institutions don’t have a monopoly on expertise. But it is cult-like and not conducive to intellectual debate.

It is beholden on those who make bold claims to provide a steelman of what they are arguing against. And their confusion should not be considered evidence of a faulty theory or model. If someone mocks a simplified explanation of a complex phenomenon on the grounds that it “doesn’t describe reality”, then they are in fact mocking themselves. I appreciate that these points are aimed more at Steve’s followers, rather than Steve himself. But he also has a responsibility as a public educator.

The Money Multiplier model is pretty redundant now, so failing to understand Steve Keen’s position won’t keep me up at night. But I hope this article serves as as a useful record of his imperfect conduct in a debate in which some are seeking clarity, and others practice sophism.

Against MMT

The famous joke about Modern Monetary Theory is that it is not modern, not monetary, and not a theory. Which is quite funny. And yet it’s gone from being an esoteric position held by an assortment of oddballs to becoming a fairly established rationale for fiscal dominance and increasingly prevalent.

I am open to the idea that there is an important insight contained within MMT that hasn’t been fully captured by the mainstream of the economics profession. This is in part based on the fact that I don’t fully understand John Cochrane’s fiscal theory of the price level but suspect that it is helpful, and in part because I am a heterodox economist myself and don’t ignore ideas just because they’re badly espoused.

Indeed, I’ve recently engaged with several MMT advocates on X/Twitter and now feel as though I have a good understanding of the appeal and the sources of confusion.

MMT rests on elaborate wordplay.

For example,

“Taxes don’t fund a state with its own central bank and fiat currency. They allow the state to buy goods and services without causing inflationary pressures in the wider economy by depriving the non govt sector spending power.”

In other words,

“Unless you want inflation, government spending requires taxation.”

Similarly,

“Taxes do not pay for government spending.”

Sure, but,

“Taxes are required to offset the inflation that would otherwise be caused by the central bank money creation used to fund that spending.”

Sometimes, MMT provides a concise and appealing simplification. Others, a lengthy and seemingly sophisticated exposition. But a laser focus on the economic concepts reveals that it’s word play. Jonathan Bartlett has called this "technically true but practically useless" (see here for more).

MMT says “we won’t run out of money”. But “we might have massive inflation”. Which is pretty much the same thing, if we think in terms of purchasing power.

After all, inflation is a tax. It’s a tax on money balances. And our cash holdings are wealth. So inflation is a wealth tax. As “Mr Red Eagle Trader” has pointed out,

Trump's Tariffs

I find it hard to pay close attention to President Trump’s reckless and illiterate actions but there’s no doubt that his “liberation day” tariffs are the biggest act of economic self harm since the Great Depression, and we should spend time trying to understand them.

My first response was to question whether Trump had the authority to do this. Surely the whole point of the US Constitution is to protect Americans from the whims of a single person? Indeed, Ilya Somin has made the case that the tariffs are illegal:

[the International Emergency Economic Powers Act of 1977 (IEEPA)] can only be used if… the emergency is over an issue that poses "unusual and extraordinary threat"… There is nothing unusual and extraordinary about [trade deficits]… nor do they pose any real threat.

So although the President has the power to declare a national emergency, this clearly isn’t one. While we may hope that sanity will ultimately prevail, that won’t unwind the damage that has already been done. Both in terms of the initial shock (around $5 trillion wiped off the S&P 500), potential retaliations, or the lasting consequences of such a large increase in policy uncertainty.

Firstly, let’s understand the core economics. As Alan Cole argues, some countries specialise in producing specific goods or services: Madagascar is great at growing vanilla. But they are a relatively poor island nation and do not constitute a major source of demand for American exports. Australia, by contrast, is a high income country with people wanting to buy high value aircraft and subscriptions to entertainment streaming services. American companies do well selling into that market. Australia is also very good at producing metals, but given how heavy and far away they are it makes little sense for Americans to import from them. In a world without money, economic trade would be based on barter and therefore everyone would have an equal trade balance with everyone else. Americans would need to find something they can sell to Madagascans if they want to consume delicious vanilla beans. And their exports of Netflix documentaries would be constrained by how much expensive metal they wished to buy. The reason why money is so useful is because it means we don’t have to settle for bilateral trade balances, and can instead benefit from specialisation: it makes economic sense for Americans to have net imports with Madagascans and net exports with Australians.

One might worry about having a negative trade balance overall, and being a net importer relative to the world as a whole. But this isn’t resolved by eliminating all bilateral trading deficits. And even if it were, these negative trade balances are not tariffs. The amount of money that American consumers voluntarily send to Madagascar in exchange for vanilla beans is not a reflection of “unfair” trade practices. It is not because the Madagascan government is aiding and abetting their domestic industry that American vanilla farmers struggle to compete internationally. Tariffs are bad, and should be cut where possible. And tariffs can affect the trade balance. But it makes no sense to treat the trade balance as a way to measure tariffs.

So what’s going on? Some of my academic research relates to the importance of ideological factors in explaining political leadership and while Trump is not ideological, we can try to make sense of the thought process underpinning his actions. Trump’s main fallacy is equating a trade deficit with an unhealthy economic relationship. But Steve Davies has argued that:

People saying correctly that Trump's tariffs are economically nuts miss the point. This is a political project. The principle of neomercantilism is that economic exchange should be subordinate to political ends. It is a collectivist political economy (nationalist).

I think this is correct, but even though there’s no point trying to make economic sense out of the tariffs, the calculation methods do reveal two very important things: (1) economic logic has been thrown out the window; (2) this is policymaking by AI.

Let’s consider those “reciprocal” tariffs (full list here):

On X/Twitter, @orthonormalist seemed to be the first person to work out the rationale (summarised by @Geiger_Capital here):

It’s simply the nation’s trade deficit with us divided by the nation’s exports to us.

White House Deputy Press Secretary Kush Desai pushed back, saying this was incorrect and the calculations were based on this seemingly more complex formula.

Bear in mind that a country’s exports (x) minus their imports (m) is also known as their “trade deficit” and that we need to be consistent about whether we’re looking at the perspective from the US or the country we’re imposing a tariff on. Then, when you consult the official “Reciprocal Tariff Calculations” you find that:

• The price elasticity of import demand, ε, was set at 4

• The elasticity of import prices with respect to tariffs, φ, is 0.25

So it isn’t just that the analysis is economically nonsensical, these clowns don’t even understand what they are doing! Possibly because they outsourced the exercise to a LLM, which also explains why many locations that aren’t countries, but do have their own IP configuration, were included.

Clearly, the values for ε and φ are crucial. The official document uses a paper (Cavallo et al, 2021) as justification for φ being “low” but don’t provide that citation in the references. I assume that this is the paper the White House were referring to, but it finds that:

tariffs passed through almost fully to US import prices, implying that much of the tariffs’ incidence rests with the United States.

So although tariff passthrough to retail prices might be low (as per the White House), the impact on import prices is much higher. In fact, Kevin Corinth and Stan Veuger argue that the elasticity should be 0.945, not 0.25. This affects the analysis by a factor of 4 and would imply that almost all tariffs should be at the arbitrary and Chat-GPT generated 10% lower bound. Madness.

Consider the following scenarios:

1. Trump is an idiot, surrounded by sycophants.

2. Trump and his team realise they have 2 years to achieve as much of their agenda as possible, and are unleashing a deliberate whirlwind of executive orders to overload the courts and hope that some of it sticks. Ultimately, however, common sense will prevail - a combination of grown ups, special interests, and the legal system will roll back many of the policies and the long term health of the US (and global) economy will depend on his successor.

3. Trump and his nepotistic cabal are deliberately trying to damage the economy so that they can benefit from having shorted it.

4. Trump is a Russian agent and is just doing what Putin wants him to.

5. Something else is going on.

I am not sure which is worse. 1 is Occam’s Razor, and consistent with most of the facts. 2 is perhaps the optimistic take, and I think there is some good evidence in its favour. 3 sounds too much like an unfounded conspiracy theory for me - there are much easier ways for a President to improve their personal finances than via sabotaging their economy (and I don’t deny that Trump isn’t doing these as well) but wiping trillions of the stock market is not consistent with a theory about rich billionaires getting away with whatever they want. I think we should be paying close attention to any evidence in favour of 4, but don’t see how these tariffs benefit Putin per se. If anything - and much more of a concern to me - they benefit China.

This thread by Students for Liberty does a good job of articulating scenario 5, arguing that tariffs are being used by the Trump administration as a way to achieve two objectives: (1) retain the dominance of the dollar as an international reserve currency; (2) improve export competitiveness. Ordinarily countries would use conventional monetary policy tools to walk this tightrope, and it is therefore telling that Trump is publicly calling for interest rate cuts. For now, however, he is forced to use tariffs because he has more control over them. What we are seeing is something common across the world and throughout history:

• Tariffs as an important form of tax revenue collection

• Fiscal dominance (where political leaders seek to use monetary policy to support their fiscal objectives)

The issue is that these are typically associated with poor, corrupt economies with little state capacity and a lack of independence in important public bodies (such as the central bank). We are not used to such techniques in America.

The final point I wish to make is a broader one. Some people have tried to draw a link between the neoliberal economic doctrine and the rise of the populist right. I wonder what type of intellectual gymnastics are required to maintain the view that MAGA have any intellectual lineage to the “globalists”, now that JD Vance is explicitly justifying trade policy as an effort to retreat from a “globalist” approach. It is also popular to consider America to be an oligarchy, governed by business interests. If that were the case, financial markets would be in charge. Clearly, they’re not. Perhaps America is becoming a plutarchy, or a “tech-bro”-ucracy. But these aren’t variants of capitalism. At their core, the dominant MAGA ideology is now old school Marxism: “pulling for a fundamental remaking of the economy to bring about redistribution of income to the proletariat from the globalist elites. They now hate the wealthy, except those working for Trump…” (h/t Ivan Pongracic on Facebook). Of course, the difference with Marxism is that in a socialist democracy those at the top were supposed to be working in the public interest. And while I think Bernie Sanders has far more integrity than Donald Trump I am not sure how much that matters - this is a populist revolt against the basic rules of global capitalism. It is a radical effort to “bring back” manufacturing and short circuit financial markets. It rejects Economics 101 and the principles of comparative advantage, market prices, and free trade. It is deeply depressing and signals the importance of understanding the basic insights of what constitutes a free society. The collectivists are winning.

Assessing Milei's impact

When I teach Macro Policy I make the following bold claim to students:

“It is relatively simple to achieve macroeconomic stability, if policymakers wish to do so.”

Perhaps this glosses over the political challenge of implementing reforms, but I believe that the science of economics gives us the technical knowledge about how to stabilise an economy. The implication is that instances of macro instability are simply a result of bad policy, and countries can stabilise quickly if their leaders want to.

In December 2023 Argentinians elected Javier Milei to be their President, providing an almost perfect test of my claim. This is a country with awful macroeconomic performance, and a policy maker who is myopically committed to radical economic reforms. If ever there were an experiment to see what impact a crazy economics teacher can have, this was it.

I didn’t know much about Milei before his election, although I am somewhat familiar with his intellectual influences and circle (he is an anarcho-capitalist, not a populist!). Indeed I was excited to hear about his intention to dollarise the Argentinian economy and “burn down” the central bank. I am a longstanding critic of central banks and find monetary reform plans that involve dollarisation to be promising. Some good examples include:

• Greenwood, J., Hanke, S., and Zalles, F.,  "Dollarize Argentina; Abolish the BCRA" Studies in Applied Economics, Johns Hopkins, November 2023

• "How to Dollarize Argentina" by Nicolas Cachanosky, October 9th 2023

• "Pro Dollarization" by John Cochrane, November 14th 2023

Indeed one of those authors - Nicolas Cachanosky - is someone I know and have co-authored with. And he has worked with people within Milei’s team. So I was very interested to see what was going to happen.

As it turns out, despite taking a “chainsaw” to deregulation, and utilising his executive powers to make a series of bold and ambitious reforms, Milei rolled back on his rhetoric about the monetary system. I think this demonstrates a degree of pragmatism, and is probably sensible. And it also means we can make a more meaningful judgment about his macroeconomic stabilization plan.

Macro stabilization

When I run my “Macro Policy Workshop” I use this video to introduce the basic concepts:

The main point is that if we assume that the objective of monetary policy should be to control inflation, and that the objective of fiscal policy should be a sustainable public debt burden, then the implied policy response is really quite simple:

• Don’t print too much money

• Don’t spend more than your raise through tax revenue

Not only simple to understand, but also simple to achieve. Stop printing money, and stop spending too much!

So let’s see how Milei fared, one year on. Is it really as easy as I imply?

Inflation

As mentioned, Milei retained the Peso and therefore needed to restore Argentina’s foreign currency reserves. This complicates his use of monetary policy, but he’s clearly put a break on the printing press. The chart below shows that M2 growth stabilised after December 2023.

Indeed, upon taking office Argentina was heading toward hyperinflation, and yet this trajectory almost immediately reversed course. As the inflation data shows, Milei has brought things under control.

Public finances

Major cuts in government spending have meant that Melei started to deliver a primary budget surplus from his very first month in office. There can be no doubt about the intent to restore fiscal discipline with such a remarkable turnaround in spending.

The point of a budget surplus is to help stabilise the burden of public debt, and so ultimately the debt to GDP ratio is key. We can see below that public debt exceeded 150% of GDP in 2023, but is now forecast to fall. This will ultimately depend on whether IMF and other institutions support Milei’s reforms, and whether spending cuts harm future growth. But this is quite dramatic progress towards more sustainable public finances.

I was amazed to see how quickly Milei was able to reverse these two critical economic indicators, and the success with which he has curtailed inflation and restored budget discipline. This vindicates the claim that macro policy can be quite straightforward. That said, we should also consider the impact on other important indicators; and other policy objectives.

Other macro indicators

My expectation was that austerity would have a negative impact on GDP, and therefore Argentina would enter a downturn. In fact, although GDP fell 2.3% in Q3 2024 relative to 2023, it rose by 3.9% compared to the previous quarter, thus breaking the technical definition of a recession. The IMF think real GDP growth will be 5% in 2025. Combined with low inflation this is the very definition of aggregate demand stabilization!

In Milei’s first quarter in office unemployment jumped from 5.7% to 7.7% but has fallen since then, down to 6.9% in Q3 2024. Unemployment data is relevant because it represents such an important concept, but is not of direct control by policymakers and subject to all sorts of measurement difficulties. The fact that the macro stabilization has not led to dramatic increases in the headline unemployment rate is therefore a pleasant surprise.

I think the main criticism of Milei’s reforms is the impact on poverty, and the official rate has increased from 45.2% to 52.9%. This has been presented as a serious flaw in his radical agenda, and requires analysis. I’m not an expert on how poverty is measured, and how much weight to put on the indicator, but I think context is important here. An 8 percentage point increase in poverty is alarming, but when the base is so high it’s clear that Milei’s actions aren’t the main problem. Indeed back in 2015 the poverty rate was 30%, showing that it is a long term issue and an increasing trend line. Milei’s claim is that by tackling inflation this should help poverty reduction going forwards, and this seems reasonable. Indeed, if you were to argue that he should ignore inflation and prioritise increased government spending as a means to reduce poverty then you have the economic platform of the previous regime, and that is what created this mess in the first place!

The final indicator I think worth mentioning is country risk, as this reflects general confidence in the economy as well as the government’s ongoing borrowing costs. The FT reports that under Milei this has fallen from 2,000 basis points to 750 and is critical for Argentina’s ongoing solvency. In terms of results, we can give Milei a quick scorecard:

• Inflation: 🟢

• Budget deficit: 🟢

• Public debt: 🟠

• GDP growth: 🟢

• Unemployment: 🟠

• Poverty: 🔴

• Country risk: 🟢

Structural policy

Although I think that is is relatively easy to achieve macroeconomic stability, this is a necessary but not sufficient condition for good economic performance overall. If policymakers achieve positive and stable aggregate demand this means that you avoid any booms or busts, but tells us nothing about general improvements in living standards. Ultimately, the most important economic indicator - real GDP growth - is determined by factors outside the amount of spending attributed to the central bank or finance ministry. What matters is how that public money gets spent, and the structural policies that intend to increase the long run (potential) growth rate.

Milei is in crisis mode, and it would be an error to prioritise long term decisions. He needs policies that have an immediate impact. But given how successful the stabilization has been, it is natural to consider the underlying factors that determine future growth. I am not sure whether Milei’s emphasis on austerity is due to an ideological battle against the state, or a practical expectation that doing so will be conducive to economic productivity. And I am concerned about the collateral damage caused by extreme policy reforms. But the status quo were clearly untenable. So I am optimistic. When it comes to a 4 year retrospective, I hope the Argentinian economy is robust and the Argentinian state is capable of performing its necessary functions. At least now that looks possible.

Update: May 2025

The poverty rate fell to 38% in the second half of 2024, which is below where it was when Milei took office. This should count as very good news for the people most critical of his “shock therapy”, and allow them to support his efforts to transform the economy!

---

Recommended further reading:

• Argentina: has Javier Milei proved his critics wrong?, Financial Times, December 10th 2024

• Javier Milei - my 1 year review, Maroz.com, November 19th 2024

• Javier Milei and Argentina's Economic Challenge, Mises Institute, August 28th 2024

Recommended podcast:

For an interview with Milei, where you learn more about his intellectual background, see here:

The Economist on R*

I was interested to see that this week’s “Free Exchange” is about estimating the natural rate of interest (R*). The Economist points out that one way to infer the Fed’s views is to subtract the target inflation rate from the dot plot projection of long run interest rates. In their September 18th update of the 19 officials involves there were 11 different forecasts (ranging from 2.38% to 3.75%). They point out a 2021 paper by Claudio Borio (which you can read here) which finds a notable increase in attention for the natural rate from top policymakers.

Borio also has a 2024 paper surveying various estimates (read it here) which are summarised in this chart:

The key takeaway seems to be that a lack of consensus around these estimates should make policy makers wary of relying on it as a consideration. Indeed The Economist concludes:

Aiming for an imaginary and almost certainly false variable is just as likely to hurt as to help. In that sense, the collapse of consensus in the Fed’s r-star projections is welcome. It is a form of intellectual honesty.

But this just begs the question - then what instead? I think monetary aggregates have proven a useful guide throughout the recent inflation but this view is contested. Indeed any criticism of how central bankers attempt to conduct monetary policy should consider the fact that it may be a fool’s errand overall. After all, the best response to nihilism is to accept defeat and give up.

Macro Trends: Live and online

I’ll be delivering a live webinar on Monday November 20th, 5pm UK time. The focus will be on Macro Trends with some commentary on the main policy stance across the Eurozone. This is an experiment to see if there’s sufficient demand from students and interested non-students for ad hoc extra content, and I’m looking forward to it.

The link is here: https://escp-eu.zoom.us/j/95163589937

Edited: The original version of this post said 6pm. Apologies.

R* at 2% for the UK for 2023 Q2

Back in 2020, the journal ‘Economic Affairs’ published an article of mine that attempted to estimate the natural rate of interest for the UK economy. I followed Beckworth and Selgin (2010) to provide a rough approximation using the following formula:

In other words, the neutral rate today is equal to the long run steady real interest rate (set at 2%), plus the difference between expected Total Factor Productivity Growth, and the long run average TFP growth rate. The average is calculated as follows, with λ = 0.7:

I haven’t given it much attention since then, but I recently received an email from someone asking if I could update the figures, which I’ve done. The natural rate is of 2023 Q2 is estimated to be 1.9%, having slumped to -12.3% in 2020 Q2 and then bouncing back to 10% in Q3. Further evidence that covid times need to be looked through, somewhat, and why level targets are more important than growth ones. The r* estimate from 1998-2023 looks like this:

If we wish to look at the last 5 years, we can see the following:

This is obviously a rudimentary estimate and should be used with caution. But I hope it’s a useful contribution to the conversation about taking the natural rate more seriously.

Have the Bank of England lost control?

Last Thursday the Bank of England increased interest by half a percentage point, to 5%. As you can see, the recent trajectory and pace of interest rate changes have been significant:

The rationale is simple: the primary job of the Monetary Policy Committee (MPC) is to keep inflation at around 2%, and it has remained stubbornly high. As you can see over the last 3 years, the conventional measure of inflation has been on a strong upward trend.

My explanation for what’s happened rests on a few claims:

• The initial impact of Covid was primarily a negative demand shock, (not a supply shock), which therefore put downward pressure on prices. There was a necessity for monetary policy and fiscal policy to be accommodating and expansive.

• Policymakers seemed to have learned their lesson from the global financial crisis by responding to the collapse in total spending by allowing subsequent spending to rise quickly. Rapid growth in the economy in 2021-2022 was necessary and important to return to the previous trend line.

• The challenge was always going to be ensuring a “soft landing”. If they withdrew demand too quickly, we’d slip back into recessionary territory. If they failed to withdraw it early enough, we would have entrenched inflation.

• Clearly Central Banks were naive about the extent to which high inflation in 2022 was driven by aggregate demand as opposed to supply side issues relating to post covid bottlenecks, and shocks to energy prices caused by Russia’s invasion of Ukraine. They’ve been complacent and have reacted to the threat of inflation too late.

• Now, there’s a real danger of an overreaction. We can already see that inflation is subsiding. Once more interest rate rises flow through into the real economy, there’s a danger that by avoiding +10% inflation we fall below the 2% target, and cause a major and unnecessary slowdown.

Back in December 2021 I discussed whether central banks were listening to those who argue that trend rates are more important than growth rates. I was hopeful, but consider this chart, published by David Beckworth in September 2022.

You can see three really important things:

1. In 2008/09 policymakers allowed NGDP growth to fall below where it needed to be to ensure neutral monetary policy, and for several years it stayed there.

2. In 2020 policymakers ensured that after NGDP growth fell below the neutral path it was then allowed to quickly catch back up again (big success!!)

3. As of 2022, however, it was overshooting and way above the rate required for monetary neutrality.

The above rests on my preference for using stable growth in the cash value of economic transactions (NGDP) as the optimal monetary regime. But you don’t need to advocate NGDP targets to be concerned by current central bank decision making.

When I teach monetary policy to MBA students I use an exercise called “Monetary Implications” which shows how to assess decisions from 3 perspectives. We can do the exercise now:

1. Money growth rule

   Broad money growth has been slowing for some time and is now just 1.6%. Divisia money growth is an even bigger concern, contracting by -2.9% in April.

2. Inflation target

   As already shown, inflation is high. CPI is growing at 7.9% and core inflation seems worryingly stubborn.

3. NGDP target

   2023 Q1 saw growth of 6.6% which is higher than the average prior to covid (which was around 4%), but it has fallen in every quarter since the start of 2021. The MPC don’t explicitly target NGDP so there’s no reason to think they are paying close attention to it. But my major concern is that the current path of interest rate rises will reduce total spending such that NGDP continues to fall below the long term appropriate rate of around 4%.

Here’s a summary:

If all three alternatives point in the same direction, policy decisions are non-controversial. The problem now is that money growth data and inflation data provide two polar opposite implications for policy. If we use NGDP as a decider, I think that the greater concern for downward trend probably means that we should be more cautious about waiting for the consequences of previous interest rate decisions to pass through. These are strong reasons against raising interest rates. Even more importantly, the real focus should be on market expectations regarding where these indicators are heading. If it’s the case that inflation expectations have become dislodged from the 2% target, while NGDP expectations are also on a decline, we have a truly terrible situation where we’ve chosen the wrong policy objective and failed to even achieve that. Scary times ahead.

Finally, I’m not a monetarist, but I think it’s important to acknowledge those who’ve been warning about high inflation for some time, and also when they stopped worrying about it. I’ve been using this chart for the US since January 2023:

It shows high a big increase in M2 preceded the rise in inflation. It also shows that M2 subsequently became negative, and that inflation was starting to fall.

Here’s data from the UK from mid 2022. Once again, and as standard old fashioned monetarism implies, the inflation measure follows what happens to the money supply (in this case I use a Divisia measure). If we expect that relationship to continue, our concern is about falling inflation not persistently high inflation.

Raising interest rates under the current circumstances seems to be a case of too much, and too late. Things would have been better had the MPC taken inflation more seriously in 2021, but that’s in the past. They shouldn’t make a new error in response.

A quick and clear growth recipe

I think the recent political turmoil affecting the government stems from two key things that they’ve done:

1. Advocating economic growth as a policy ideal without providing a coherent plan to deliver it.

2. Neglecting the difference between campaigning and delivering, and buying into the myth that fiscal discipline can be abandoned under certain circumstances (permitting large increases in public debt in a pandemic, when interest rates are very low, is fiscally sensible. Unfunded tax cuts outside of a crisis situation, is not).

Although I am surprised, and still a little confused by the strength of the market reaction, I am also a little reassured that the Cameron/Osborne’s prioritisation of fiscal consolidation has been somewhat vindicated. (One can argue on whether austerity was the right way to achieve that, but they were not wrong to warn about the dangers posed by markets losing confidence in credible public finances). That said, the new Chancellor’s strong signal of a return to pragmatic attention on short term tax fudges as a mean to permit limitless spending intentions is a real shame. I liked Truss’s optimism, and agree that there are lots of ways we can move onto a higher growth trajectory. We shouldn’t fall back into a low growth mindset that leaves the UK on a slow march to social democratic tax burdens and substandard infrastructure and public services. Here are what I would priorities as part of a quick and clear growth recipe:

1. Build homes - we need to unlock the housing market to allow people to move where their labour is most productive and start to unwind the unhealthy concentration of personal wealth within property. The fix must come from the supply side and focus on planning reforms that enable more houses to be built.

2. Generate power - our shift toward clean energy and away from geopolitical hostility has always had an obvious solution, which is investment in nuclear power. The fracking debate seems an unfortunate distraction where the real focus should be on SMRs and fusion reactors.

3. Boost trade - the EU constitutes our largest, richest and closest market and finding ways to mitigate the costs of Brexit are crucial for future growth prospects.

4. Encourage talent - the best way to mitigate the problems associated with a demographic trend of an ageing population is encouraging more immigration. For high skilled labour this is win-win and

The above would contribute to a quick and clear impact on growth, but they aren’t necessarily easy. There are reasons why existing inefficiencies and problems become entrenched, and there seems to be a reduced appetite to take them on. I am contributing to the first problem mentioned above with such a rudimentary list of ideas. The real difficulty is implementation and the politics of reform. And regrettably good economics is often bad politics. But one thing we can do is unite around a growth agenda, and publicise the good ideas that would contribute to that.

Does the UK economy look on the verge of a currency crisis?

No.

The recent market reaction to the mini budget has prompted wider discussions about the potentially perlilous state of the UK public finances. In this post I want to provide some clarity on what constitutes a “currency crisis”, and how the typical warning signs help to illuminate the current UK situation.

A currency crisis is routinely used to describe situations where a currency loses a lot of value relatively quickly. However this definition is vague, and when the trigger for quick market movements is a political speech, in the context of a highly polarised and poorly motivated public discourse, it is unhelpful. When I teach my MBA students we use this classic Harvard case and apply the following definition:

A 10% or more fall in the value of a currency, within a week, relative to a suitable external benchmark.

This poses three questions: how much value is lost? over what time period? and relative to what?

Prior to 2016 I told students that by using this definition it is almost impossible to imagine that a currency crisis can occur to a floating exchange rate. When the value of a currency is set by demand and supply, on a competitive market, it would take a ridiculously large shock to prompt such a dramatic and immediate reappraisal. Therefore our discussion in class is focused almost entirely on countries that have some sort of fixed exchange rate, where the crisis is the moment at which authorities abandon their target. In other words, while there are many causes of a currency crisis, the trigger is almost always the abandonment of a fixed exchange rate.

Then, in 2016, we had the results of the Brexit referendum and the UK pound lost more than 10% of its value, relative to the USD in a day. So much for useful rules of thumb!

Some minor quibbles would be at what points we are measuring the rise and fall (i.e. should we only compare an average daily rate, the rate at the end of the trading day, or the most extreme moments within any trading period); and the relevance of the external benchmark. By definition, a fixed exchange rate will have an obvious external benchmark (whether that’s the USD, the Euro, or a clearly defined basket of other currencies). For a floating exchange rate we make a choice.

Indeed the danger of focusing too much on the GBP/USD exchange rate is that it can be hard to distinguish between the weakness of the pound and the strength of the dollar. Most currencies have been weakening against the USD and so we aren’t seeing entirely UK news that is influencing that ratio.

I think it’s better to focus on a trade weighted composite index (i.e. the effective exchange rate) and using BIS figures this is what’s happened recently:

The mini budget isn’t a step change here, but if we take the level on Sep 22nd and read through until the trough, which was September 28th, that’s a 4% fall. So no currency crisis.

Having said this, taking the GBP/USD is also sensible, but as Reuters points out this is ~8% fall. So still not a currency crisis.

Of course foreign exchange markets were not the only arena of disturbance, and it’s telling that as the pound has recovered more attention has switched to gilt yields. These are a more useful macroeconomic indicator because they provide a reflection of the premium the UK government is required to pay investors in be willing to buy their sovereign debt. Gilts spiked following the mini budget and it is because of the ramifications that this had to pension companies that prompted the Bank of England to intervene, calming things down.

https://www.cnbc.com/2022/09/28/bank-of-england-delays-bond-sales-launches-temporary-purchase-program.html

So I think it’s overblown to call these events a “currency crisis” and would require a clear definition from those who claim otherwise. But this leads us to the main point of this post, which is to consider whether indicators are suggesting that a currency crisis may occur.

The simple answer (Brexit referendum result to one side) is of course not, the GBP is a free floating currency! Indeed the very large price adjustments being made recently reduce the necessity for big swings later. This is the market doing it’s job: rapidly incorporating new information such that single events have less importance. The underlying causes of why a currency is losing its value get incorporated drip by drip, rather than all at once.

That said, we can go back to my MBA classroom discussions and consider the standard list of indicators that might forewarn about an impending currency crisis:

1. Is the current a/c deficit over 5% off GDP? - when a country imports more than they export they tend to run a current account deficit. For many relatively wealthy countries being a net borrower is no bad thing - it means consumers get access to more products, and we have inflows of foreign investment. A typical rule of thumb is that 5% of GDP amount to a “large” currency account deficit. According to the ONS the current account deficit has been quite volatile recently but most recent data (for 2022 Q2) shows -5.5% (down from -7.2% in Q1). So it’s large, but it’s not deteriorating. Direction can be as important as overall size. I’d say this is flashing orange.

https://www.ons.gov.uk/economy/nationalaccounts/balanceofpayments/timeseries/aa6h

2. How is the current account deficit being financed? - it’s one thing to run a large currency account deficit, but if the predominant source of inward foreign investment (which is being used to finance it) is formed of Foreign Direct Investment (i.e. in fairly large and stable projects like building factories) then there’s little risk of a sudden reversal. By contrast, if the deficit is being funded by portfolio flows, which are prone to sudden reversal, then we’d be more concerned. According to the ONS we can see outflows of portfolio investment but at declining rates over the last few quarters. Inward FDI has been quite stable, and other investment (i.e. short dated bonds) are positive and stable. This looks green to me.

3. How large are reserves? - if sources of inward investment dry up, the key question is whether the government can continue to fund its current account deficit through other means, such as the use of foreign reserves. One of the key indicators that Vladimir Putin was going rogue was his steady stockpiling of international currency, since 2015, reducing dependency on voluntary trade and international cooperation. On the contrary, if a country has a low amount of international reserves, or begins haemorrhaging them, it is a sure sign they are losing control. UK foreign exchange reserves have steadily increased since the global financial crisis, and given that a free floating exchange rate doesn’t require any reserves to manage the stability of the currency, this represents a strong position.

https://www.ceicdata.com/en/indicator/united-kingdom/foreign-exchange-reserves

4. Is the real exchange rate deteriorating? - if a country has a fixed exchange rate then it fails to serve as an indicator of impending devaluation, but the real exchange rate will provide more of a clue given that it adjusts for inflation. As shown, an effective exchange rate is a good indicator of general trends, and the trajectory is a concern for the UK. Rather than treat the real exchange rate as indicator, however, we can just look at inflation. The current inflation rate using the traditional CPI basket (which is what the Bank of England use to determine monetary policy) is 9.9%. The CPIH measure, which adjusts for types of housing cost, and is the primary focus presented by the ONS, is 8.6%.

This is obviously way above the target rate of 2% but is subsiding and the general consensus seems to be that the Bank of England are starting to apply the brakes such that it will not remain elevated for long. When using inflation as a predictor of a currency crisis, however, we shouldn’t confuse cause and effect. Rather than viewing the inflation rate as a sign of potential currency deterioration, it is in fact another view of the same problem. While a fall in the exchange rate is measuring the currency against an alternative currency, a rise in inflation is measuring it against a basket of goods and services. These are simply two different ways to revealing the same common issue - a reduction in purchasing power.

5. Is the budget deficit out of control? - According to the ONS, in the first quarter of 2022 the budget deficit was 2.6% of GDP which is smaller than the EU27 average and within the 3% threshold typically deemed to be a red flag. There is a more recent publication, showing a more detailed look at public sector finances, released in September, but I’m not aware of a stable link for a more timely snapshot of the fiscal position. The key issue, of course, is where this is heading. The NIESR forecast the deficit will rise to 8% in 2022/23 and we are still awaiting confirmation of when the OBR’s updated forecasts will be made public. Either way, the deficit is contentious partly because it relies so much on growth projections and what goes into the GDP calculation can have much of an impact on the outlook as any claims about spending relative to tax revenue. For now, however, the warning lights are green.

Public debt rose dramatically during the pandemic and for good reason. Despite recent rises in yields debt isn’t high in comparison to equivalent historical circumstances, and prior to Truss/Kwarteng we’ve all been repeatedly led to believe that debt remains cheap and easy to finance. That can change quickly, but there’s room to manoeuvre.

As a classroom exercise, and looking at publicly available data, there are no clear warning lights indicating an imminent currency crisis. And we should not be surprised - floating exchange rates don’t have currency crises. But the real art is taking more timely, pertinent indicators and anticipating sudden changes in market sentiment. Indeed the main conclusion from my MBA class is that regardless of what data we look at, we can’t reliably predict a currency crisis. So there’s no need to panic. Yet (!)

Verdict on the mini budget

I am finally catching up on the mini budget, which was announced on September 23rd. The market reaction has been almost as frenzied as the Twitter reaction, but I shall do my best to look at it constructively.

Firstly, as Ryan Bourne points out here, it reveals a strong conviction that:

a combination of marginal tax rate cuts and supply-side liberalizations of important markets will raise GDP by increasing hours worked, improving productivity, attracting more talented people and businesses to the UK, and raising net investment

I think that’s broadly accurate, but won’t be transformative. The political calculus is probably dominating the economic one. The actual growth agenda was more of an intent, in terms of:

deregulation in the provision of all of energy, infrastructure, childcare, and housing

As a work of PR, that combination of surprise announcements and vague intentions clearly struggled. But policy wise it is encouraging, and I’m broadly in favour of these types of supply side reforms. I’m honestly not sure whether the criticisms are that these are bad policies and shouldn’t be pursued, or that they weren’t sufficiently fleshed out to warrant a confident assessment about their impact on growth. Maybe the problem was that it was a “mini budget”, whatever that means.

That said, it is refreshing to see a reframing of the public policy objective from redistribution toward growth, and whether or not a 2.5% target is too optimistic, it could well serve as a useful focal point.

But that seemed to get sidestepped by the noise and chatter. I really noticed the low quality of public debate within the context of social media and increased political polarization. I saw several tweets that would be commented on and prompting great derision that had entered my feed quite long after being outdated. Imagine having a real time discussion about a football match where key events are revealed out of sequence. I’m not sure a rolling ticker is conducive to sensible analysis. People are freaking out that the pound is below $1.06, but it wasn’t. A 3% depreciation is big, but how much has it fallen over the last 6 months? Are these events or continuing trends?

I also noticed the odd situation where the left used the immediate response from financial markets as a judgment of the validity of the plans. It would be absurd for them to argue that a positive verdict from financial markets should be an objective of a budget. Maybe they would argue that for a Conservative budget, where the stated objective is to stoke markets, such attention is justified because it reveals that the policy has failed on its own terms. I’m not so sure though. I wish people would identify their success criteria before they, or their political opponents, announce something…

Putting the various reactions to one side, the main point I’d like to make is that in isolation most of these measures are pretty sensible. The main criticism, therefore, is about (i) choosing priorities; and (ii) how the plans were presented and communicated. But firstly, let’s look at the pros.

The pros

• “Moving house” tax - stamp duty is stupid and everyone agrees. Cutting stamp duty isn’t the best way to improve the housing market, but it does, at the margin, improve allocative efficiency, which is good. As Paul Johnson said, “Perhaps a smaller change that we might have hoped for from such a radically tax cutting chancellor, but welcome nonetheless”. A key priority for any government should be moving toward a system where we tax property/land values rather than property transactions, and any attempt to reduce stamp duty is to be commended.

• Corporation tax - corporation tax is a hobby horse of mine because it’s such a counterintuitive policy. Superficially it appears like an alternative to taxing labour, but not only does a large share of the incidence fall on employees, it contributes to the inefficient ways in which we tax capital, which in turn harms labour. And UK corporation tax is particularly bad. No sensible economist would advocate a large increase (i.e. 6 pp) in corporation tax as we head into a recession, therefore it’s perfectly reasonable to take the opportunity to maintain the current rate at 19%.

• Income tax - this is where most of the headlines have focused, but the fact that these are the “biggest tax cuts in 50 years” also tells us something about how high the starting point is.

• Revoking planned increases in NICs is a good move and has been largely ignored in the analysis because it’s a good move.

• It also seems a good idea to scrap IR35 (which forces companies to withhold tax from self-employed labour as if they were permanent employees).

• Reducing the basic rate from 20% to 19% is a meaningful policy to help typical workers, and a step in the right direction. I would like to see larger tax cuts for lower rate payers, but notice that more than twice as much of the “cost” of this budget is from cutting the basic rate rather than removing the top rate.

• Removing 45% top rate - this is probably a useful way to encourage high productivity workers to increase output without forsaking a large amount of potential revenue. I’d have liked to see more simplification, particularly with the absurd marginal rate of 60% on income over £100,000 (which occurs because the personal allowance is removed above that amount), but there clearly is some attention to the costings here.

Overall, some would argue that this isn’t sufficiently targeted at lower income taxpayers. I agree with this, but the fact that the chart below became so widely shared reflects a really stupid approach to the debate. Of course tax cuts disproportionately affect people that pay more tax. Of course people that don’t pay tax won’t benefit from a tax cut. Come on.

There also seems to be something refreshing about a Conservative budget so clearly focused on undoing policies that were controversial at the time. Let’s not forget that when Labour introduced the 50% top rate in 2009 it was supposedly an emergency response to the global financial crisis. There was no strong economic case for such a high marginal tax rate and it would have been highly controversial outside of such serious conditions. When the subsequent Tory/LibDem coalition reduced it to 45% this seemed to take the psychological edge off the punitive rate, but was hardly a return to an optimal amount. A top rate of 40% is not particularly high, and by removing an entire band a welcome step toward simplification occurs. Labour turned this into a political football, and I think it’s strategically understandable for Truss’s team to send a credible commitment that such gestures get swiftly undone once power changes hands. Perhaps it incentives both sides to engage in sensible policy rather than contentious point scoring.

Cons

Regardless of how desirable those announcements are, in isolation, however, let’s consider the two big counterpoints.

• Choosing the the wrong priorities - the headline tax figures are all focused on the top end and that presents bad optics in a cost of living “crisis”. To be fair to Truss, however, she is an incoming Conservative Prime Minister and Tories are going to Tory. I would have liked to see more focus on poverty reduction but we shouldn’t ignore the previously announced energy price cap (which may actually be a more sensible policy than I first feared, given the difficulties in targeting direct support where it’s needed). Maybe I am paying attention to the wrong vocal critics of the mini budget, but I’ve struggled to see a viable and plausible alternative being proposed.

• Bad expectations management - the big lesson should be the importance of traditional public finance responsibility - the encouragement of independent impact assessment and some form of baseline forecast. I think a large part of the market reaction was the disregard for any fiscal rule and lack of attention to costings. And this is what I find most interesting about the issue. If Cameron/Osborne held an overly tight commitment to fiscal discipline (arguably overstating the threat from financial markets for unfunded spending commitments) then May/Hammond/Johnson/Sunak all took a hybrid position of paying lip service to Conservative commitments to fiscal prudence while in practice demonstrating immense profligacy. (Perhaps profligacy is the wrong word here - recent Conservative spending is insufficient in some areas that desperately lack investment, and is entirely justified given the Covid-19 pandemic and situation in Ukraine). The difference with Truss/Kwarteng is the complete sidestep of fiscal concerns in the favour of a bigger growth perspective. In doing so, they actually reveal that 2010s austerity might not have been such an unnecessary act of self harm. It almost feels as if they’ve seen how Labour have behaved in opposition, downplaying market discipline, and flirting with MMT, and thought “sod it, let’s do the same.” ERROR.

I think it’s uncharitable to conclude that these plans are chaotic and have been exposed as lacking coherence (of course an alternative narrative is circulating, that the Pound crash was a deliberate ploy, because Kwarteng used to work for a hedge fund. This ties into an existing conspiracy theory relating to how Brexiteers supposedly profit from economic chaos. It’s interesting, but thus far unproven. Personally, I don’t see evidence that the market response was the intention).

Interpreting the market reaction isn’t straightforward, but Ryan Bourne provides the most thoughtful response that I’ve seen:

Working out the precise economics of why we saw the combination of the falling pound and rising gilts is difficult to parse from financial market data, but can only really logically be explained as a fear in markets that the UK might engage in “fiscal dominance,” with the Bank of England eventually being too permissive on inflation, and keeping rates too low, to help out a government with high and rising debt.

This means that I also have some sympathy for the view that the markets reaction is in part an assessment of the Bank of England’s ability to deliver a soft landing.

Kwarteng: here are our plans. Assuming the Bank of England does their job, it shouldn’t have a reckless impact on inflation.

Bailey: hmm, we’ll let you know what we think of all this in November.

Ultimately, this mini budget is a fascinating reversal of typical strategy, which ordinarily sets out spending commitments and then attempts to retrospectively finance them through some combination of tax rises or additional borrowing. Instead, we see a clear focus on taxation, and spending plans are (thus far) treated as a secondary consideration. I think this is the right way round, although such a radical decision may have surprised and jolted market response. But let me outline a possible scenario:

• Truss doubles down on a growth objective

• The political legitimacy of the Conservative Party rests on achieving it

• Usual resistance to serious supply side reforms is weakened

It’s bold, naive, and possibly reckless. But if you have identified low productivity growth as the biggest problem facing the long term prosperity of the British people, it might be a gamble worth taking.

Note: The two best insights on Truss’s economic policies are Ryan Bourne and Julian Jessop. I highly recommend their commentary.

The higher inflation survival guide

One of the key issues facing the global economy right now is the extent to which present inflation is a temporary consequence of supply chain disruptions, or the long awaited consequence of more than a decade of emergency monetary policy. Regardless of the proximate or underlying cause, the data is clear: inflation is high and rising:

This is important. Central bank competence rests on their credibility - i.e. do the public believe that they will achieve their stated objectives? And I think we can split credibility into two elements:

1. Their capability to fight inflation. Since the global financial crisis central banks have obtained a whole suite of new tools to conduct monetary policy in different ways. For example, a “corridor system” uses three different interest rates to guide policy and was introduced in large part to mitigate the risks of QE.

2. Their commitment to fighting inflation. Historically the Fed in particular have been behind the curve in responding to fast changing macroeconomic conditions. Now that the Fed and the ECB have greater room to permit inflation to go above target, it becomes less certain that they will act early and decisively to quaff it.

Personally, I am confident that central banks have the tools to prevent inflation getting out of control, but I have more doubts about their commitment. It’s therefore worth considering how to proceed if inflation continues to rise.

The purpose of this post is to consider some of the implications for managers.

How to deal with inflation: revenues

The obvious response to how managers should respond to inflation is to raise their prices. But of course that is what inflation is. It’s not a plan.

One option is to follow the lead of the Japanese ice cream company who, in 2016, released this video to apologise to their customers for having to raise the price from 60 to 70 Yen (see here for more):

But don’t forget that there are alternatives to raising prices. Akagi Nyugyo could have:

• Reduced the amount of ice cream contained in a serving

• Used lower quality ingredients

So firms need to make adjustments to their products and their pricing.

Inflation also poses a much deeper problem. If the economy were always in equilibrium, inflation wouldn’t matter. Higher total spending would cause all prices to move instantaneously, and relative prices wouldn’t change. In the real world, however, problems occur because some prices rise faster than others. Typically, revenues are more flexible than costs, and therefore inflation boosts profits and encourages (unsustainable) expansion.

Inflation therefore poses a real problem to entrepreneurs. They have to solve “the signal extraction problem”, which asks the following question: “what proportion of any increase in demand for your products is due to consumers placing a higher value on them, and what proportion is due to inflation?” It’s an impossible question to answer, but an important one to ask. How much of your profitability should you attribute to successful entrepreneurial activity, and how much is a reflection of wider macro events?

How to deal with inflation: costs

The main justification for positive inflation targets rests on that fact that wages (i.e. the “price” of labour) are particularly slow to adjust. Few people want their wages to perfectly track economic conditions, because we like to have some financial stability. Many people’s salary is only adjusted once a year, and labour markets are therefore much slower to adjust than things like commodities or share prices. This generates a macroeconomic problem, however, because the labour market is so important. One way to enable people’s real wage (their actual purchasing power) to adjust, without relying on firms to change their nominal wage, is through inflation. If central banks engineer system wide positive and moderate inflation (e.g. 2%) then employers can reduce their (real) costs without having to reduce anyone’s pay packet. So it is important to be careful with automated cost of living adjustments. If your business has consistent performance, and you want to ensure that your employees receive the same actual compensation, you must increase their nominal payslip in line with inflation. (But don’t forget that the signal extraction problem is boosting profit and thus overstates performance). For companies that are struggling right now, and need to cut costs, inflation provides scope to do so. Afterall, it isn’t corporations who cause inflation, it is central banks. Central banks are the one to blame.

That said, we are still in competitive labour markets and across the board wage freezes are a terrible strategy for your high productivity employees. So I was particularly interested to see Lance Wigg’s advice on coping with inflation:

• Invest more time in benchmarking salaries and recognise these need to be updated more frequently

• Early career employee’s market value will change more quickly than others, so they need more frequent reviews

• If you are worried about losing talent don’t be afraid of paying more than the market, and then allowing inflation to catch up later

Looking beyond labour markets, his further advice includes:

• Buy expensive items earlier in the cycle than you were previously planning

• Minimise cash holdings

• Move toward index linked debt

Finally, inflation is very tough on groups that have fixed incomes and (often) lower salaries. As a society we should recognise these costs of inflation and hold central banks to their mandate of protecting us from it.

Did the NGDP crowd win the battle of ideas?

Perhaps not, given that no major central bank has adopted an explicit nominal income (or NGDP) target. However…

I recently spent a very pleasant train journey to Turin catching up on various podcasts. This included several episodes of Macro Musings (the best monetary economics podcast by far, and one that I highly recommend), including:

• George Selgin on Bitcoin an CBDCs

• Scott Sumner on The Money Illusion

• Megan Greene on the future of CBDC and central bank mission

• Larry White on stablecoins and CBDCs

• Mark Carney on Value(s) relating to central banking

And I also noticed that Scott was talking about his new book, ‘The Money Illusion’, with Larry White on the Hayek Program podcast:

• Lawrence White and Scott Sumner on The Money Illusion

First off, I found the contrast between the practitioners vs. academics to be fascinating. I’ve learnt so much from George, Larry and Scott and consider them to be three of the most important monetary economists around. I sometimes disagree on points of emphasis, but can’t say that I ever consider their arguments to be flawed. And yet the actual implication of their work is so opposed to the reality of how central banks behave! Perhaps there’s also some context with my recent review of Mervyn King’s ‘Radical Uncertainty’, which frustrated me greatly. There’s something about central bankers downplaying the formalism of the discipline, giving attention to concepts like uncertainty or subjectivism, once they’ve finished their term, that rankles. Carney is so smooth, so confident in his analysis and reflections. And I do think his tenure was a (qualified) success. But he seems oblivious to the depth of insight that free bankers/market monetarists provide. Megan Greene is also an impressive expert, but sidesteps any consideration of public choice, mission creep, or the knowledge problem to present a confident vision of a more powerful central bank. They both provide clarity, and optimism. And I believe that knee jerk critiques are ill founded (clearly there’s scope for central banks to pay attention to climate change within their existing mandate). But just imagine the world we’d live in if Selgin, White and Sumner had the legitimacy and authority conferred by high office …

I haven’t yet read ‘The Money Illusion’ and although I intend to, I suspect I’m familiar with the key points. In terms of these interviews, here are some good points that Scott made, across both of those podcasts, that I hadn’t fully considered before now:

• The Fed is usually operating behind the curve. In other words, the natural rate moves faster than their response. That being the case, cutting interest rates are more likely to indicate tight policy than loose policy and raising rates will coincide with loose monetary conditions. More recently, there’s evidence that the Fed are more forward looking, and this implies a major improvement in policy.

• The natural rate of interest (R*) can move quickly in a crisis. I’d add that this is in large part because central bank incompetence affects it. This is the “supplier induced demand” argument I made in the chapter of ‘Getting the Measure of Money’ relating to velocity shocks.

• Advocates of fiscal policy can be unclear on how they define and use the term ‘liquidity trap’. If it simply means that interest rates are low, and that there’s high demand for base money, then it does indeed exist. But there’s nothing about this situation that implies monetary policy has become ineffective. The issue is whether policymakers have sufficient credibility to use the monetary policy tools necessary to raise nominal growth expectations. Some commentators may favour fiscal policy because they don’t believe that (typically) conservative central bankers will do “whatever it takes”. But the optimal strategy is to hire central bankers that know how to do their job.

• Scott argued that we shouldn’t expect central banks to be able to forecast recessions because if we can predict them, we can prevent them. As he has shown us, however, events in 2008 demonstrate that central banks don’t always prevent demand side recessions. Therefore, in trying to predict a recession, we are really trying to predict central bank incompetence.

• Despite being an Austrian-school economist I don’t like to use the term “bubble”, and try not to violate EMH. I do think we can talk about “booms” (as in the manifestation of loose monetary policy), and about the difference between primary (Austrian) and secondary (Monetarist) recessions. But Scott argued that many “bubbles” can be plausibly explained by fundamentals:

  • The 1990s stock market (especially Nasdaq) only made sense of US tech firms would come to dominate the global economy - they did!

  • The 2000s housing market only made sense if we would be able to rely on very low interest rates and NIMBY restrictions on new housing construction to generate a secular rise in house prices - which is exactly what happened!

What I found most interesting was Scott’s optimistic take on the influence of NGDP targets. He made a few key points:

1. A flexible average inflation target is one way to permit NGDP playing a role without the embarrassment of abandoning an inflation target.

2. The Fed’s decision to cut interest rates in 2019, despite inflation being high, indicates an increased concern for market expectations (see falling inflation expectations here) and a triumph of market monetarism.

3. We’ve now got back to the pre-covid NGDP trendline (see David Beckworth’s charts, shown below) which is why this recession hasn’t prompted a debt crisis.

This, in the context with being attributed as “the blogger who saved the economy”, due to the influence he had over the Fed’s late 2012 QE3 program, is a cool achievement. Scott deserves this recognition, and he’s a hero.

My own take, however, is a bit more pessimistic:

• Scott emphasises that it’s the level targeting he’s really interested in, not NGDP per se. In which case it might have been a strategic error to focus so much on NGDP when other economists were advocating price level targets (see Chapter 1). Personally, I want to move away from giving consumer prices such an important role in policy decisions and so I’m wary of pinning too much hope on level targets per se.

• Although an average inflation target approximates a level target over a suitable time horizon, it provides much more discretion and relies on better decision making than if it were a clearly defined rule (i.e. an explicit level target). There is now a lot of uncertainty about time horizons and too much flexibility is a bad thing for monetary policy. I’m worried that the Fed won’t be able to handle this additional epistermic burden.

• It’s clear that Nominal GDP data is too lagged, flawed, and large scale (released quarterly) to provide a meaningful guide for covid related policy. Scott said that we should only be looking 1-2 years ahead and that there’s no point to maintain NGDP on a month to month basis. But this presents a curious problem. One of the main advantages of an NGDP target over inflation targets is the fact that they deal better with supply shocks. If covid is interpreted as a supply shock, but can’t use NGDP data, then we’re really not contributing to the public debate. (This is why I have been using Average Weekly Earnings as a measure of nominal income rather than NGDP, but I don’t advocate using it as a policy target).

Regarding covid, Scott’s attention seems to be more on unemployment data than inflation data and seeing in the former real problems associated with health risks. In this situation, stimulating normal incomes won’t help much because although it would create inflation it wouldn’t provide the nominal receipts required to prevent the downsizing that occurs in a traditional recession. He therefore thinks it’s ok to let NGDP contract sharply, provided there’s a commitment to get back to the previous trend path over a reasonable time period.

Scott considers it to have been a massive unanticipated real shock that monetary policy shouldn’t be expected to do anything about. But if that’s the case it should put upward pressure in inflation. In the UK, inflation didn’t exceed 1% throughout 2020 and has jumped from 2.1% in May 2021 to 4.2% in October. This implies two things to me:

• There’s been a lag, and the inflation has only showed up in the data following the reopening of the economy (and the interplay between Brexit and covid re supply chain disruptions). Or

• The immediate impact of covid was an unusual demand side recession caused not by a fall in confidence (the typical Keynesian explanation) but by a government mandated fall in spending.

When we entered the first lockdown and saw widespread mothballing my inner Austrian was warning against an assumption of a quick recovery because I felt people were underestimating the intricacies of the supply chain and the capital disruption that would occur. Keynesian appeals to hysteresis can be complementary to Austrian attention to capital heterogeneity (which tells us that recessions take time to correct and cause real damage). However, Aggregate Demand clearly fell in 2020.

Even if you treat 2020 as a demand “problem” it still doesn’t imply that monetary policy was wrong. Imagine that a nuclear superpower invades a sovereign European nation, drawing the US and UK into a third world war. The UK government dramatically ramps up military spending such that measured GDP grows. In such as a case, we would prioritise winning the war over ensuring stable nominal income growth and a temporary boom may be a necessary side effect. Perhaps a similar argument can be made regarding covid - that it’s not a failure of NGDP targets to ignore them in extreme circumstances, and that such instances necessitate government to do more. I don’t think we have the state capacity for government spending to (temporarily) offset the reductions in private sector activity during lock down, so we just put this down to force majeure.

***

When I sat on the IEA’s ‘Shadow Monetary Policy Committee” I struggled to find the balance between interpreting the brief as “what I would do given the remit and constraints faced by central bankers” and “what I’d like to do if I were in charge”. Therefore, I was fascinated to learn that Mark Carney himself admitted to (partially) neglecting the inflation target in order to follow the implications of an NGDP level target. He said that Osborne’s letter (e.g. here, from 2015) that reminded him if the flexibility over time scale gave him the scope to see through some types of temporary deviations from target. What’s really telling, however, is that this is subtle, and being revealed now. But the outcome is clear, and was suspected - if you look at q-on-q4 growth of NGDP from 2010 (with Carney's tenure starting around the orange line) you do see better performance, with 4% NGDP growth +/- 1%.

So, let me close by quoting Carney’s parting words to David Beckworth:

I hope we get your nominal GDP target some day

Some may argue, we no longer need it.

Monetary conditions

I’m not paying close attention to the debate about monetary policy at the moment, but I routinely update the following table which attempts to assess the current situation from three different perspectives: (1) those who advocate money growth rules; (2) those who advocate inflation targets; (3) those who focus more on NGDP. As you can see, recent CPI data is causing great concern, but monetary aggregates and nominal income remain stable.

Kaleidic Guide 2021 edition

The updated Kaleidic Guide to UK Monetary Policy has been recently updated. It’s available to buy, as a hard copy, or to download, for free.

Who to follow on Twitter

To keep on top of the UK monetary policy debate, here are who I consider to be the best people to follow on Twitter:

• Chris Giles - Economics editor, FT

• Claire Jones - Global economy report, FT Alphaville

• Tim Wallace - Deputy economics editor, The Telegraph

• Julian Jessop - IEA economics fellow

• Tony Yates - Commentator

• Frances Coppola - Commentator

• Jonathan Portes - Professor of Economics, King’s College London

• Andrew Sentance - former MPC member

• Rupert Harrison - Portfolio manager, Blackrock (former advisor to UK Chancellor)

• EconHedge - Hedge fund guy

Understanding NGDP targeting

Last night I participated in an ASI Webinar on NGDP targeting. You can rewatch it here.

I was flattered to appear alongside the Scott Sumner, ‘The blogger who saved the economy”, and enjoyed the event. I thought I’d post my notes here.

What is an NGDP target?

Instead of being bound by a money growth rule or an inflation target, the central bank conducts monetary policy to hit a specified rate of nominal income. This aims to create a stable environment for wage and debt contracts, which are more important for economic planning than stability around consumer prices. It would allow inflation to rise when real growth is low, and potentially for prices to fall when productivity is strong.

How can NGDP targets fit within a free market approach to monetary policy?

Some would argue that having a central bank that undertakes monetary policy is fundamentality incompatible with a “free market” approach. But given that we have a central bank it’s reasonable to try to reduce the harm that it can do. And it’s potential harm works in two directions: (i) excessive inflation (and in some cases hyperinflation); and (ii) allowing expected nominal incomes growth to collapse (as happened in 2008).

Not only do I believe that an explicit NGDP target would improve central bank performance, it moves us closer to a free market solution.

• It’s neutral - NGDP stability is a means to delivery monetary equilibrium, which occurs when the supply of money adjusts to changes in the demand for real balances. (In terms of the equation of exchange, it’s desirable for changes in V to be offset by changes in M such that PY remains stable. Indeed this is what would occur in a “free banking” regime, without a central bank). Monetary equilibrium will move interest rates toward the “natural” rate, which is where the demand and supply of loanable funds is in equilibrium, and ensure an efficient allocation of resources.

• It’s limiting - If tied to open market operations (OMO) you can strip away a lot of central bank activity that’s distortionary, and this limits the central bank to it’s only legitimate role, which is managing the supply of that which it has a monopoly over.

• It’s rule-based - If tied to market expectations (e.g. by setting up an NGDP futures market) you eliminate any discretionary decision making by central banks, reducing the epistemic burden of monetary policy.

How has the Bank of England responded to the global financial crisis, Eurozone sovereign debt crisis, and covid-19 pandemic?

Their response has been wedded to a failed approach to monetary policy. The Bank of England pioneered “One Target One Tool'“ and have historically been committed to a very simple framework where they use interest rates to target inflation. In addition to adopting QE in 2009, the Bank have utilised a range of ad hoc tools but with no stated objective or clearly communicated exit strategy. They have also been inconsistent on whether they have an inflation target (e.g. aim for 2% inflation in 2 years time) or a price level target (e.g. aim for 2% inflation, on average, over a certain time horizon). They’ve introduced unemployment as a threshold for forward guidance and there’s even a claim that by “seeing through” inflation when real growth is low, they have an implicit NGDP target. Either way, it’s long overdue that they adopt a new approach.

Is now the right time for NGDP targets?

2008 showed NGDP targets in all their glory - a negative supply shock prompted inflation to rise and central banks responded with tight monetary policy (the ECB famously increased interest rates to 4.3% in July 2008. You can’t really blame them for that, however, because they were following their commitment to an inflation target). This is the classic situation where inflation targets and NGDP targets have different implications for monetary policy, and NGDP targets are superior.

Initially I interpreted the coronavirus pandemic as a supply shock, and therefore thought that NGDP targets may have another moment of focus. However it’s increasingly obvious to me that we haven’t had a negative supply shock at all - there’s no fall in capacity and the labour force is largely undamaged. Rather, it’s been a very odd type of demand shock. We haven’t seen a fall in people’s desire to spend money per se, but we have seen a state mandated reduction in economic activity, which amounts to the same thing. (It isn’t really a Keynesian collapse in confidence, but technically it constitutes a fall in people’s desire to spend money, or, equivalently, a rise in people’s desire to hold money). Hence we’ve seen large increases in the savings rate, household deposits, and repayment of consumer credit. (Indeed this is why many are optimistic about the recovery - normally in a recession there’s a case for government to “kick start” spending with a fiscal stimulus, but the fiscal multiplier is irrelevant now. All that’s needed is permission to spend).

Given that we’re facing a demand shock, which puts downward pressure on inflation, there’s less necessity for an NGDP target. It wouldn’t imply a different policy response than the existing inflation target. So I don’t see a reason for much appetite for an NGDP target right now, and won’t hold my breath. That said, I believe an NGDP target is even more relevant than in 2008, for three key reasons:

• CPI data is faulty - we know that the current “basket” of goods used to measure inflation won’t reflect the huge changes in consumption patterns that have taken place due to lockdown. The large drop in transactions and impact of legislative restrictions on things like price gouging mean that central bankers will be taking CPI data with a large pinch of salt.

• Better suited to ensuring financial stability, which is of increasing concern - the counter cyclical inflation caused by NGDP targets cause real debt burdens to change in a pro-cyclical manner, and shares the losses with the creditor. This is good.

• We already do it (sort of) - some argue that prior to 2007 there was an implicit 5% NGDP target being adopted. It isn’t a massive jump to make the output part of any “dual mandate” more explicit, and uniting it with the inflation target to create a simple, combined focal point.

Ultimately I believe we’re long overdue an end to “emergency” monetary policy, and now’s as good a time as ever to move to an NGDP target.

What are the downsides of an NGDP target?

• It relies on GDP data which is slow to be released and subject to revision. Some argue that overly tight policy in 2008 was more due to faulty GDP data than a commitment to an inflation target, and you don’t want monetary policy hampered by large revisions to past data.

• The “total income stream” doesn’t care whether spending is captured within GDP so there may be better measures to target. You could opt for something narrower (e.g. consumption of final goods) or broader (e.g. total transactions). Ultimately though I believe that all macro indicators have limitations, and right now GDP figures are no worse than the CPI basket. And there’s a trade off to be made in terms of how well known GDP is and understood by the public. I’m monitoring Average Weekly Earnings as a key indicator for the UK, but I’m not ready to abandon GDP is our key macro indicator just yet.

• Leads to greater inflation volatility, and it was a hard fought battle to create independent central banks that see fighting inflation as their primary aim. We don’t want to return to a time when inflation is highly volatile. And yet adopting an NGDP target would, I believe, continue to keep inflation expectations well anchored. As we’ve seen since 2008 inflation can swing quite widely above and below target when we fail to achieve macro stability. An NGDP target would bring greater stability and ensure that although inflation does more “work”, it operates within a reasonable range.

• It doesn’t work for all countries - for small, open economies that are reliant on single commodities an NGDP target isn’t suitable. For such countries I’d recommend other monetary policy regimes - e.g. a currency board, or fixing to an alternative nominal anchor. But I think an NGDP target works well for large industrialised countries with independent, credible central banks.

In my proposal for an NGDP target, published as “Sound Money”, I advocated a 2% average growth of NGDP expectations over a 5 year rolling period.

I note that in Scott Sumner’s latest paper, published yesterday, he advocates the following:

the Government should provide the Bank of England’s monetary policy committee a remit to:

• target a nominal GDP growth of around 4% per annum over the coming years;

• use “level targeting,” which means making up for past undershoots or overshoots — in practice, this would mean compensating for lower nominal GDP growth in 2020 by targeting a higher nominal GDP growth rate in 2021; and

• have the central bank target market expectations of nominal GDP growth.

Also yesterday, the former Chancellor Sajid Javid included the following recommendation in his report on restoring growth post covid:

• the Government and the Bank should consider a shift in its remit from targeting inflation to nominal GDP, in order to better deliver sustained growth.

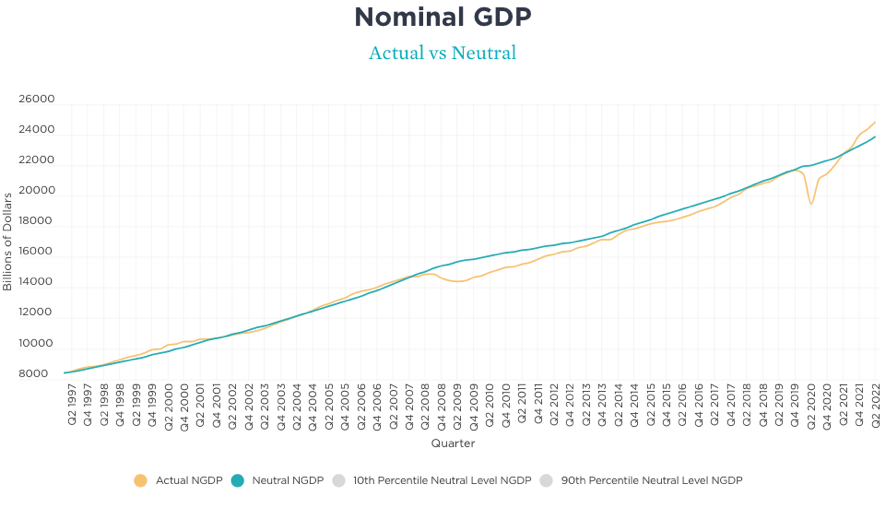
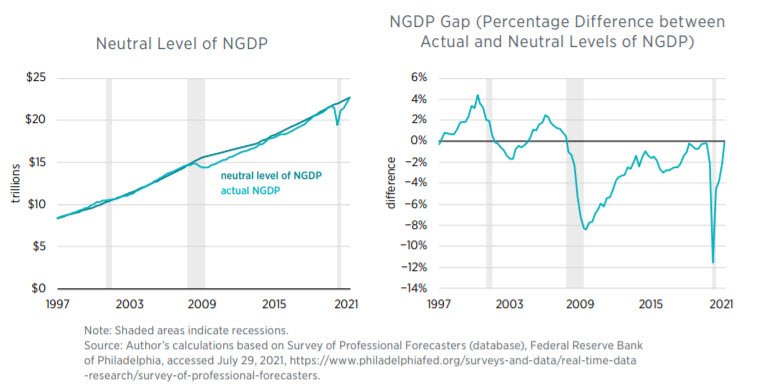
Astute watchers will have noticed that David Beckworth was originally supposed to participate, but unfortunately he wasn’t able to join the webinar. Fortunately though he’s produced this timely analysis of NGDP Targeting in the UK.

So yesterday was a big day for NGDP targets in the UK. Let’s hope the momentum builds!

Not dead yet: the future of monetary policy

I recently read, with great interest, the Resolution Foundation’s “Recession ready? Assessing the UK’s macroeconomic framework”. Written by James Smith and three co authors, I was in the mood for a broad and solution-led survey of how monetary, fiscal, and structural policy might be reformed. But it shouldn’t take 113 pages to say “when monetary policy becomes ineffective use fiscal policy instead”. I know that I’m being a little harsh to suggest that’s all they do, but I can’t help but feel that the Keynesian conclusion can be readily anticipated from the Keynesian premise, which is “what tools do we need to escape a future recession?” The alternative approach would be to ask “what macroeconomic framework will prevent recessions from occurring” - a deeper question, and one which may well lead to different answers.

I totally accept that low interest rates have caused a major problem for the Bank of England, but only to the prevailing approach of inflation targeting. An attack on the status quo isn’t an effective criticism of monetary policy more generally. The report pays lip service to a higher inflation target, and more systematic QE (something I approve of), but seems keen to dismiss those as minor tweaks to an approach that didn’t adequately draw attention to fiscal policy. But demonstrating that different fiscal policy improves on current monetary policy is not a fair fight.

(As an indication of the pernickety way in which I read the report, Figure 3 reveals that “Recessions always result in falling GDP and rising unemployment”, but a recession is falling GDP. Also, Figure 32 claims to show that “tax receipts have fallen since the financial crisis”, but given that it shows receipts as a proportion of GDP, it could also label this as “GDP has risen”.)

To consider how to fix monetary policy, such that we’re not left with fiscal policy as a last resort, I recommend “Facts, Fears and Functionality of NGDP Level Targeting: A Guide to a Popular Framework for Monetary Policy”, written by David Beckworth and published by the Mercatus Center. This is the paper I’d been hoping he’d write for some time, covering the basic idea behind a nominal GDP target, as well as dealing with some common criticisms.

The first criticism he deals with is how to respond to changes in the potential real GDP growth (Y*). If we set an NGDP target of 4% (let’s say we want ~2% inflation and believe the long term growth rate of real GDP is 2%), then what happens if a productivity slowdown reduces Y* to 1%? Beckworth points out that there’s two options. The first is to recalibrate the NGDP target, e.g. by bringing it down to 3%. But he also mentions George Selgin’s preference, which is to allow the trend inflation rate to change instead. I see three main reasons to favour the latter: (i) by permitting inflation to rise to 3% you are utilising the price systems ability to signal information, rather than be used as an arbitrary means to shape expectations; (ii) a little inflation volatility is tolerable given that by adopting an NGDP target you’ve already decided that nominal income stability is more importance than price stability; and (iii) in this situation you’d need to adjust an inflation target anyway.

The second criticism is that data revisions make NGDP targets impractical. I think this is a valid concern - CPI data is more immediate and reliable than GDP figures - and I don’t find Beckworth’s reassurances totally convincing. His first counterpoint is that a Taylor rule also requires an estimate of GDP (and potential GDP to boot), but this is precisely why many policymakers avoid using it. Certainly in a UK context I believe MPC members place much more weight on the latest CPI figures than on their impression of the output gap. Beckworth’s second counterpoint is that there are ways to improve our real-time estimates. He suggests using income data, or high-frequency nowcasting (such as that used by the Atlanta Fed), or credit card companies payments systems. I’m intrigued by this, and looked into payment data in my book on alternative monetary indicators (see chart below). But whenever I read people getting excited by the possibilities of big data my Austrian instincts kick in and I question whether a lack of data, or computing power, has ever been the constraint on central planning? And even if big data would help, it isn’t ready yet. And I want an NGDP target now! His third counterpoint is my favoured approach, which is using markets rather than computing power - in particular Scott Sumner’s proposal for an NGDP futures market. But it’s never been clear to me how such a futures market would deal with revisions to past GDP figures. (It seems to open the door to policy changes in response to revisions to past data, but this may just be a downside of any level target.)

UK payments growth (% change on previous year)

The third criticism that Beckworth responds to is that the public won’t understand NGDP targets, and I like Beckworth’s framing of a “dollar income growth” as the improvement over a “cost of living index”. But this does cut against the political difficulty of having to wind back an overshoot. In the same way that it’s difficult to sell a need for higher prices to the public during a downturn, it would not be popular to put the breaks on wage growth when the economy is strong.

Finally, Beckworth made a strong case in favour of the financial stability angle of NGDP targets. As he says,

the countercyclical inflation created by an NGDP level target will cause real debt burdens to change in a procyclical manner

This is a big improvement on the status quo. Currently, a recession means that prices fall and the real debt burden on debtors is increased. Under NGDP targets a downturn will lower the real debt burden and share some of those losses with the creditor. Beckworth points to empirical literature showing this risk sharing is useful in a world of incomplete financial markets.

Two bold papers, both worth reading.

Getting the Measure of Money

The IEA have recently published my book on UK monetary policy, called "Getting the Measure of Money".

Throughout the last century or so, economic theory and history have marched together. At certain times, in certain places, new ideas (and the new packaging of old ideas) have captured the attention of the public and policymakers, and been adopted. At other times, and in other places, experiences have prompted an appetite for something different. Arguably, for much of the twentieth century we have seen the latter – the perceived failure of the existing system has required something new. The experience of the 1930s led to the rise of Keynesianism. The experience of the 1970s led to the rise of monetarism. I believe that the experience of the 2008 financial crisis has led to an ongoing revival in Austrian economics. Whilst I do not anticipate the Austrians matching the scale the Keynesian and Monetarist revolutions, the book is my modest attempt to help, by applying some specific Austrian insights to a UK context.

2012 saw the centenary of the original publication of Ludwig von Mises’ The Theory of Money and Credit. I wrote an article (co-authored with Robert Thorpe) that was published in the Review of Austrian Economics, justifying Mises’ position as a quantity theorist. We argued that Mises’ understanding of the equation of exchange differs from both of the conventional textbook versions, and warrants recognition as being a distinct contribution. Most importantly, the equation of exchange can be utilized for distinctly Austrian analysis.

Austrians might argue that you can’t show the business cycle in an aggregated way, but I would argue that the equation of exchange is still the best way to approach it. Indeed according to Ludwig Lachmann, “Austrian aversion does not pertain to these aggregates as such… It pertains to the construction of an economic model in which these aggregates move, undergo change, and influence each other in accordance with laws which are devoid of any visible reference to individual choice” (1978, p.8). It therefore isn’t non-Austrian to utilize economic aggregates, provided they have adequate microfoundations. As Cachanosky (2009) has pointed out, Mises rejected the use of price indices for pure theory. However,

“Their application is appropriate for history and politics. Catallactics is free to resort to them only when applying its theorems to the interpretation of events of economic history and of political programs. Moreover, it is very expedient even in rigid catallactic disquisitions to make use of these two terms whenever no misrepresentation can possibly result and pedantic heaviness of expression can be avoided” (Mises 1949 [1996], p.423).

According to Egger (1995), Athur Marget was a neglected economist because he became known purely as a historian of the “Quantity Equation”, and this focus on aggregate variables was at odds with claims of being attentive towards methodological individualism and subjectivism. However Egger goes on to argue that Marget helped show that the “conceptual organisation” of the “Quantity Equation”, is “capable of the disaggregated, individualistic, and subjective analysis of temporal process that has always identified the Austrian method (Egger, 1995, p.20)”.

Finally, the aim isn’t to provide a definite “Austrian” account of the crisis, because that is simply too ambitious. Indeed as Opper (2002) says an intention to provide one would be falling into the same trap as the mainstream of the profession,

“it appears that the wholesale rejection of Austrian ideas in the post-war era went too far. This rejection reflected a drive by the economics profession to develop a detailed theoretical macroeconomic framework that applied to all business cycles, a goal that is now recognized as overly ambitious”

Rather, if you are engaged in UK monetary policy debate, but are worried that our standard indicators are misleading, this book shows what the Austrian school can add. Data and appendices are available on my personal website.

The defence lines for the war on cash

The Cato Institute has recently published a paper by Jeff Hummel, called “Should Governments Restrict Cash?” As you should expect it’s an excellent overview of the topic and contains multiple astute insights. Hummel considers the two main cases for abolishing cash - (1) to crackdown on criminal activities; and (2) as a means to conduct monetary policy. He notes that some economists stress the former (Larry Summers) and some the latter (Willem Buiter) and his central target is someone who advocates both - Kenneth Rogoff.

Hummel persuasively argues that the burden of proof should fall on those who want to abolish cash to demonstrate that the benefits of doing so would outweigh the costs. And I think he’s right to point out that thus far they’ve neglected a number of important insights. Such as:

• Actual welfare analysis needs to take place which distinguishes between wealth creating black market activity and wealth destroying illegal activity.

• Inflation is a tax on real money balances and therefore is currently used as a tax on illegal activity. Therefore going cashless would alter the tax rate facing criminals.

• The highest denominated banknotes provide the highest amounts of seigniorage. Abolishing them would therefore impact public finances.

• The US Dollar is a global public good and affects welfare in dollarised countries as well as non-dollarised countries. There’s no evidence to say that restricting the ability of Russian criminal gangs to use US banknotes would compensate for depriving normal Russian families of diversifying from Ruble holdings.

I’m open minded about the so called “war on cash” and conscious of the fact that my instinctive support for anonymous forms of payment cuts against the potential for central banks to solve coordination problems in systems where they are in fact the monopoly provider or currency. However Hummel nicely presents where the defense lines are and since they’re yet to be breached it seems clear that monetary economists have an obligation to protect people’s rights to use cash.